Dynamic Programming: Solving Subproblems by Steps
Author: Yongfeng Gu, Date: May, 2020
Dynamic Programming (DP) is a widely-used strategy in Computer Science, whose core idea is decomposing the original problem (often large and complicated) into several subproblems (often simple and easy to compute). That is, DP won't directly compute the original problem at once but turn to solve its subproblems iteratively. This blog gives three representative problems (i.e., Knapsack Problem, Levenshtein Distance, Longest Substring Problem) that can be solved by DP.
1. Knapsack Problem¶
The knapsack problem aims to find a subset of $n$ items, each of which has a value $v_i$ and a weight $w_i$, under the total weight limit $W$ meanwhile achieve the maximum value. Suppose the basic information of $n$ items are as follows,
| Attribute | item 1 | item 2 | item 3 | item 4 | ... | item n |
|---|---|---|---|---|---|---|
| Value | $v_1$ | $v_2$ | $v_3$ | $v_4$ | ... | $v_n$ |
| Weight | $w_1$ | $w_2$ | $w_3$ | $w_4$ | ... | $w_n$ |
The problem can be formulated as (where $T$ denotes the subset of selected item index),
$$ maxmize \sum_{i\in T}v_i \\ s.t., \sum_{i \in T}w_i \geq W, \ v_i > 0, \ w_i > 0 $$How to present the solution? To solve the Knapsack problem, we first number these $n$ items from $1$ to $n$ and select from $1$ to $n$. Then, we define a symbol $D(i,j)$ to denote the maximum total values after making $i$ selection decisions (select or deselect an item). Here $j$ denotes the total weights after making $i$ selection decisions. Hence the solution of the Knapsack problem can be represented as $D(n,W)$. That is, once we obtain the value of $D(n,W)$, we solve the Knapsack problem.
How to calculate the $D(n,W)$? - Actually, we cannot directly calculate its result but we can use the idea of Dynamic Programming to recursively decomposite the $D(n,W)$ into an easier expression (e.g., $D(1,1), D(1,2)$) to calculate. In other words, we must construct the relationship between $D(n,W)$ and $D(n-1,W)$ (or something like $D(n-1,W-1)$).
How to extract the relationships? - Take $D(i,j)$ for example, it means the after making $i$ decisions, we can get a total weight of $j$. Suppose that the $i$-th item's weight is greater than $j$ (i.e., $w_i>j$), which indicates that the $i$-th item should not be selected. Thus, we have a relationship $D(i,j) = D(i-1,j)$ if $w_i>j$. Suppose that the $i$-th item's weight is less than $j$ (i.e., $w_i<j$), which means that the $i$-th item can be selected or deselected. If we selected the $i$-th item, the total value $D(i,j)$ equals $D(i-1,j-w_i)+v_i$. Otherwise, $D(i,j)$ equals $D(i-1,j)$. To maximize the total value of $D(i,j)$, we always select the max value of that two possiblities. Overall, the relationship within $D(i,j)$ is as follows,
$$ D(i,j)= \begin{cases} D(i-1,j), \ \ \mbox{if} \ w_i >j \\ max \begin{cases} D(i-1,j-w_i)+v_i, \ \ \mbox{select the i-th item} \\ D(i-1,j), \ \ \mbox{deselect the i-th item} \end{cases} \end{cases} $$Under the above relationships of $D(i,j)$, we can construct a look-up table to save the $D(i,j)$. In this table, the left-top is $D(0,0)$, which means the maximum value by selecting 0 items. The right-bottom is $D(n,W)$ (final solution).
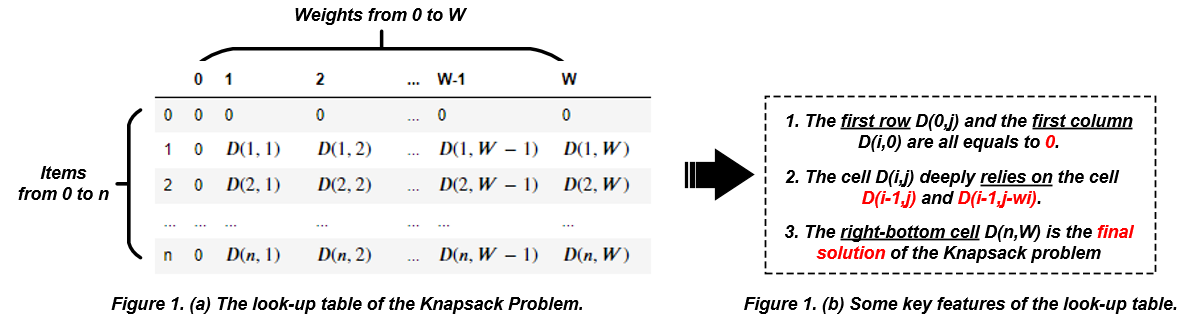
Program Example: Jack has 5 items and their values and weights are {6,3,5,4,6} and {2,2,6,5,4}, respectively. Suppose that Jack's bag can only take a total weight of 10. Please help Jack to select a subset of 5 items to maximize its total values.
| Attribute | item 1 | item 2 | item 3 | item 4 | item 5 |
|---|---|---|---|---|---|
| Value | 6 | 3 | 5 | 4 | 6 |
| Weight | 2 | 2 | 6 | 5 | 4 |
Here's a Python example (simple_knapsack()) to solve the given Knapsack Problem and return the look-up table.
def simple_knapsack(n, values, weights, W):
''' To return the look-up table of the given Knapsack Problem
Parameters:
---------------
:n: number of items
:values: value of each item
:weights: weight of each item
:W: weight limit
Returns:
---------------
:lutab: look-up table
'''
values.insert(0,0)
weights.insert(0,0)
lutab = [[0 for j in range(W+1)] for i in range(n+1)] # initialize the look-up table
for i in range(1, n+1):
for j in range(1, W+1):
if j < weights[i]:
lutab[i][j] = lutab[i-1][j]
else:
lutab[i][j] = max(lutab[i-1][j], lutab[i-1][j-weights[i]]+values[i])
return lutab
n = 5
values = [6,3,5,4,6]
weights = [2,2,6,5,4]
W = 10
lutab = simple_knapsack(n, values, weights, W)
print('Look-up Table:')
for row in lutab:
print(' ', row)
print('Maximum Values:', lutab[-1][-1])
According to the above code snippet, we can find the maximum values Jack can take is 15. Here's another example make_decision() to help Jack to make decisions (i.e., which to select and which to deselect).
def make_decision(lutab, weights):
'''To figure out which to select
Parameters:
----------------
:lutab: the obtained look-up table
:weights: weight of each item
Returns:
----------------
:decision: selection decision, 1 for select and 0 for deselect
'''
rows = len(lutab)
columns = len(lutab[0])
decision = []
j = columns-1
for i in range(rows-1, 0,-1):
if lutab[i][j] == lutab[i-1][j]:
decision.insert(0,0)
else:
decision.insert(0,1)
j = j-weights[i]
i -= 1
return decision
decision = make_decision(lutab, weights)
print('Selection Decision:', decision)
Can we optimize the look-up table? Obviously, the size of the look-up table will increase with the number of items (i.e., $n$) and total weights (i.e., $W$) of the problem, which takes a large memory consumption when the question is scaling up. One key question is can we save memory consumption? In other words, can we record fewer data in the loop-up table? Up till now, there is a sound strategy that suggests we should compress the two-dimensional look-up table into one-dimension one. The idea behind this strategy is that,
- the calculation of cell $D(i,j)$ only depends on the previous line (whatever $D(i-1,j)$ or $D(i-1,j-w_i)$).
- the calculation of cell $D(i,j)$ only depends on the left side of column $j$ in the previous line (both $j$ and $j-w_i$ are less than $j$).
Hence, an alternative method is to save the current row (i.e. the $i$-th row) of the look-up table rather than the whole rows. In each iteration, we compute the $D(i,j)$ from right to left. Here's an example to achieve this idea.
:) This optimized strategy can save memory consumption of the look-up table but it failed to give us detailed selection decisions.
def optimized_knapsack(n, values, weights, W):
''' To return the current row of look-up table
Parameters:
---------------
:n: number of items
:values: value of each item
:weights: weight of each item
:W: weight limit
Returns:
---------------
:crow: current row of look-up table
'''
values.insert(0,0)
weights.insert(0,0)
crow = [0 for _ in range(W+1)]
for i in range(1, n+1):
for j in range(W, 0, -1):
if j >= weights[i]:
crow[j] = max(crow[j], crow[j-weights[i]]+values[i])
return crow
n = 5
values = [6,3,5,4,6]
weights = [2,2,6,5,4]
W = 10
crow = optimized_knapsack(n, values, weights, W)
print('Current Row:', crow)
print('Maximum Values:', crow[-1])
One variant of the Knapsack problem is the Grouped Knapsack Problem (GKP). Different from the 0/1 Knapsack problem, GKP rules that some items are disjointed in the selection decisions, that is, all items are grouped into several classes and we can only select one item from each classes.
Program Example: Jack has the following 5 items to select, each of which has a value ($v_i$) and a weight ($w_i$). He has to select a subset of these 5 items to maximize the total values within the total weights limit ($W=10$). However, there are dependencies among such items, i.e., once Jack select B or C, he must select A.
For A, B, and C, the possible selections include {A}, {A,B}, {A,C}, {A,B,C}, which can be grouped into one class. For D and E, there is no dependency on them. Therefor, we can construct a variant look-up table as follows,

def grouped_knapsack(n, weights, values, W, dependency):
''' To return the look-up table of the grouped knapsack problem
Parameters:
---------------
:n: number of items
:values: value of each item
:weights: weight of each item
:W: weight limit
:dependency: dependency among items
Returns:
---------------
:lutab: look-up table
'''
values.insert(0,0)
weights.insert(0,0)
groups = [[]]
for i in range(len(dependency)): # get items that have no dependency
if dependency[i] == 0:
groups.append([i+1])
for i in range(len(dependency)): # split the items into groups
if dependency[i] != 0:
for j in range(len(groups)):
if dependency[i] in groups[j]:
groups[j].append(i+1)
for i in range(len(groups)): # replace the group that has more than 1 item with its powerset
if len(groups[i])>1:
p = groups[i][0]
powerset = get_powerset(groups[i][1:])
for k in range(len(powerset)):
powerset[k].append(p)
groups[i] = powerset
lutab = [[0 for j in range(W+1)] for i in range(len(groups))] # initialize the look-up table for groups
for i in range(1, len(groups)):
for j in range(1, W+1):
if len(groups[i]) > 1: # for groups that has more than 1 item
max_values = [lutab[i-1][j]]
for group in groups[i]:
t_w = 0
t_v = 0
for item in group:
t_w += weights[item]
t_v += values[item]
if j < t_w:
continue
max_values.append(lutab[i-1][j-t_w]+t_v)
lutab[i][j] = max(max_values)
elif len(groups[i]) == 1: # for groups that has only 1 item
if j < weights[groups[i][0]]:
lutab[i][j] = lutab[i-1][j]
else:
lutab[i][j] = max(lutab[i-1][j], lutab[i-1][j-weights[groups[i][0]]]+values[groups[i][0]])
else: # for the empty group
lutab[i][j] = 0
return lutab
def get_powerset(items):
''' To return the power set of items
Note that this method exhausts all possible subset of items, the complexity is O(2^n)
Parameters:
-------------
:items: items list
Returns:
-------------
:powerset: powerset of items
'''
powerset = []
num_sets = 2**len(items)
for i in range(num_sets):
str_decision = str(bin(i))[2:].zfill(len(items))
subset = []
for i in range(len(items)):
if str_decision[i] == "1":
subset.append(items[i])
powerset.append(subset)
return powerset
n = 5
values = [800,400,300,400,500]
weights = [2,5,5,3,2]
W = 10
dependency = [0, 1, 1, 0, 0]
lutab = grouped_knapsack(n, weights, values, W, dependency)
print('Look-up Table:')
for row in lutab:
print(' ', row)
print('Maximum Values:', lutab[-1][-1])
2. Levenshtein Distance¶
Levenshtein Distance is one of the most widely-used edit distances to measure the difference between two strings, which is designed by the famous Russian scientist Vladimir Levenstein in 1965. In a nutshell, Levenshtein Distance calculates the least edit times when transforming one string to another one. The edit types include the deletion, insertion, and replacement.
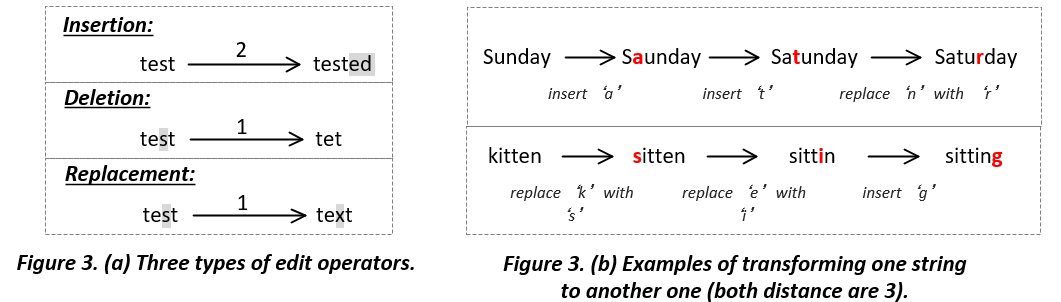
Similar to the Knapsack problem, one cannot directly figure out how many steps (deletion, insertion, and replacement) that is required to transform one string to another one. Therefore, we also decompose the Levenshtein Distance into sub-distance.
Program Example: How to calculate the Levenshtein Distance between the **_kitten_** and **_sitting_**?
| 0 | k | i | t | t | e | n | |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| s | 1 | D(1,1) | D(1,2) | D(1,3) | D(1,4) | D(1,5) | D(1,6) |
| i | 2 | D(2,1) | D(2,2) | D(2,3) | D(2,4) | D(2,5) | D(2,6) |
| t | 3 | D(3,1) | D(3,2) | D(3,3) | D(3,4) | D(3,5) | D(3,6) |
| t | 4 | D(4,1) | D(4,2) | D(4,3) | D(4,4) | D(4,5) | D(4,6) |
| i | 5 | D(5,1) | D(5,2) | D(5,3) | D(5,4) | D(5,5) | D(5,6) |
| n | 6 | D(6,1) | D(6,2) | D(6,3) | D(6,4) | D(6,5) | D(6,6) |
| g | 7 | D(7,1) | D(7,2) | D(7,3) | D(7,4) | D(7,5) | D(7,6) |
Solution: Firstly, we need to construct a look-up table (two-dimensional matrix), where each row denotes one character of the "sitting" and each column denotes one character of the "kitten". Secondly, we define the symbol $D(i,j)$ to represent the minimum distance between the top-$i$ characters in the "sitting" and the top-$j$ characters in the "kitten". Thirdly, we extract the relationships among $D(i,j)$ as follows,
$$ D(i,j)= \begin{cases} max(i,j), \ \rightarrow \ \mbox{i=0 or j=0} \\ \\ min \begin{cases} D(i,j-1) + 1, \ \rightarrow \ \mbox{insert the j-th character of 'sitting'} \\ D(i-1,j) + 1, \ \rightarrow \ \mbox{delete the i-th character of 'kitten'} \\ D(i-1,j-1) + 1, \ \rightarrow \ \mbox{replace the i-th character of 'sitting' with the j-th character of 'kitten'} \end{cases} \end{cases} $$Here's a Python example (compute_LD()) to calculate the Levenshtein Distance between two strings (words).
def compute_LD(str1, str2):
''' To return the the Levenshtein Distance between two strings (${str1} and ${str2})
Parameters:
---------------
:str1: the 1st string, e.g., kitten
:str2: the 2nd string, e.g., sitting
Returns:
---------------
:distance: the Levenshtein Distance
'''
chars1 = list(str1) # columns in the look-up table
chars1.insert(0,"0")
chars2 = list(str2) # rows in the look-up table
chars2.insert(0,"0")
lutab = [[0 for j in range(len(chars1))] for i in range(len(chars2))] # initialize the look-up table
for i in range(len(chars2)):
for j in range(len(chars1)):
if i==0 or j==0:
lutab[i][j] = max(i,j)
else:
if chars1[j] == chars2[i]: # in this case, no change should be made
lutab[i][j] = min(lutab[i][j-1], lutab[i-1][j], lutab[i-1][j-1])
else:
lutab[i][j] = min(lutab[i][j-1]+1, lutab[i-1][j]+1, lutab[i-1][j-1]+1)
print('Look-up table:')
for row in lutab:
print(' ',row)
distance = lutab[-1][-1]
return distance
str1, str2 = "kitten", "sitting"
distance = compute_LD(str1, str2)
print('Levenshtein Distance:', distance)
According to the above Look-up table, we can find that the Levenshtein Distance is 3 (the right-bottom corner), which indicates that we just only edit 3 times on the 'sitting' to transform it to the 'kitten'. However, this result is too abstract for us since we cannot know the details of the transformation. Again, we use the back forward search algorithm to figure out the details in each edit.
def extract_details(str1, str2, lutab):
''' To return the details of each edit (only print the detail information)
Parameters:
-----------------
:str1: the 1st string
:str2: the 2nd string
:lutab: the look-up table of the Levenshtein Distance
Returns:
-----------------
None
'''
chars1 = list(str1) # columns in the look-up table
chars1.insert(0,'0')
chars2 = list(str2) # rows in the look-up table
chars2.insert(0,'0')
j = len(chars1)-1
for i in range(len(chars2)-1,0,-1):
if lutab[i][j] == lutab[i-1][j-1]+1:
print('>> replace',chars2[i],'with',chars1[j])
j -= 1
elif lutab[i][j] == lutab[i-1][j]+1:
print('>> delete',chars2[i])
elif lutab[i][j] == lutab[i][j-1]+1:
j -= 1
print('>> insert',chars1[j])
else: # chars2[i] = chars1[j]
if lutab[i][j] == lutab[i-1][j-1] or lutab[i][j] == lutab[i][j-1]:
j -= 1
print("Transform from \'%s'to \'%s\'':"%(str2,str1))
extract_details(str1, str2, lutab)
3. Longest Common Substring Problem¶
The Longest Common Subtring Problem (LCS) aims to find out the longest common substring between two comparable strings. For example, string 'XYZABC' and string 'ABCXYZAY' are two comparable strings, the common substring between these two strings are 'XY', 'XYZ', 'XYZA', 'AB', 'BC', 'ABC', etc. However, among these substrings, 'XYZA' has the largest length (4) and should be the output of the LCS problem.
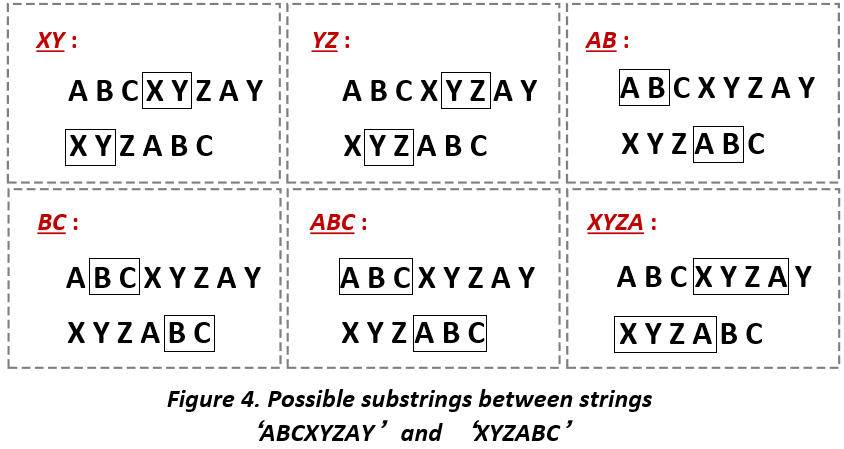
Intuitively, one may consider collecting all the substrings of 'XYZABC' and 'ZBCXYZAY' then compare each substring of two strings respectively. This method may work well on small-size comparisons but scaled to a large-size of comparisons (say the two strings both have hundreds or thousands of characters).
Fortunately, we still seek to decompose the whole problem into its subproblem. Let $N(ij)$ denote the maximum common length between the top-$i$ characters in the one string and the top-$j$ characters in the other string. Thus, we have the following relationships,
$$ N(i,j)= \begin{cases} 0, \ \rightarrow \ \mbox{if the i-th character} \neq \mbox{the j-th character} \\ N(i,j) + 1, \ \rightarrow \ \mbox{if the i-th character} = \mbox{the j-th character} \end{cases} $$Here's an example to find the longest common substring between two strings (implemented in Python).
def find_common_substring(str1, sre2):
''' to return the longest common substring of ${str1} and ${str2}
Parameters:
------------------
:str1: 1st string
:str2: 2nd string
Returns:
------------------
:substring: common substring
'''
chars1 = list(str1) # columns in the look-up table
chars1.insert(0,'0')
chars2 = list(str2) # rows in the look-up table
chars2.insert(0,'0')
substring = []
lutab = [[0 for j in range(len(chars1))] for i in range(len(chars2))] # initialize the look-up table
for i in range(1, len(chars2)):
for j in range(1, len(chars1)):
if chars2[i] == chars1[j]:
lutab[i][j] = lutab[i-1][j-1] + 1
print('Look-up table:')
for row in lutab:
print(' ', row)
max_i, max_j = find_maximum_cell(lutab) # find the position of the maximum value
print(max_i, max_j)
for i in range(max_i,0,-1):
if lutab[i][max_j] > 0:
substring.insert(0, chars1[max_j])
max_j -= 1
return substring
def find_maximum_cell(lutab):
''' to return the position (i,j) of the maximum value in a matrix
Parameters:
------------------
:lutab: matrix
Returns:
------------------
:max_i: the row index of the maximum value
:max_j: the column index of the maximum value
'''
max_i,max_j = 0,0
max_value = lutab[0][0]
for i in range(len(lutab)):
for j in range(len(lutab[0])):
if lutab[i][j] > max_value:
max_value = lutab[i][j]
max_i = i
max_j = j
return max_i,max_j
str1 = "ABCXYZAY"
str2 = "XYZABC"
substring = find_common_substring(str1, str2)
print('Longest Common Substring:', substring)
To summarize, the above three classical problems all can be solved by the idea of Dynamic Programming (DP). It is intuitive to solve a problem at once but sometimes things are harder (NP problem) than we expected. DP provides an alternative way to decompose the original problem into subproblems, which guide us to get the results by solving the subproblem by steps.